Maths Formulas for Class 8
Many students consider mathematics as a scary subject and math formulas are often difficult to remember when you don’t understand them well. The negative approach towards any subjects will make a student reluctant to study that particular subject.Usually students feel jittery during the exam time and they fail to give their best shot. To make things easier and guide through different concepts in Maths, we will discuss the important CBSE Class 8 math formulas here.
For Free CBSE Class 8 Maths Question Papers & Worksheets visit
https://www.ribblu.com/class-8-mathematics
Algebraic Expansions:
1. (a + b)2 = a2 + 2ab + b2
2. (a – b)2 = a2 – 2ab + b2
3. (a + b) (a – b) = a2 – b2
4. (x + a)(x + b) = x2 + (a + b)x + ab
5. (x + a)(x – b) = x2 + (a – b)x – ab
6. (x – a)(x + b) = x2 + (b – a)x – ab
7. (x – a)(x – b) = x2 – (a + b)x + ab
8. (a + b)3 = a3 + b3 + 3ab(a + b)
9. (a – b)3 = a3 – b3 – 3ab (a – b)
10. (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz
11. (x + y – z)2 = x2 + y2 + z2 + 2xy – 2yz – 2xz
12. (x – y + z)2 = x2 + y2 + z2 – 2xy – 2yz + 2xz
13. (x – y – z)2 = x2 + y2 + z2 – 2xy + 2yz – 2xz
Temperature Conversions :
ºC = 5959 ( ºF – 32 ) ºF = 9595 ( ºC + 32 )
Simple Interest = P X T X R / 100
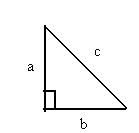
Pythagorean Theorem:
a2 + b2 = c2
Laws of Exponents
Multiplying powers with same base (Product Law)

Dividing Powers with Same Base

Power of a Power ( Power law)
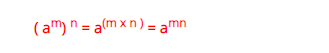
Negative Powers

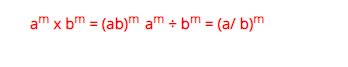
Geometrical Formula:
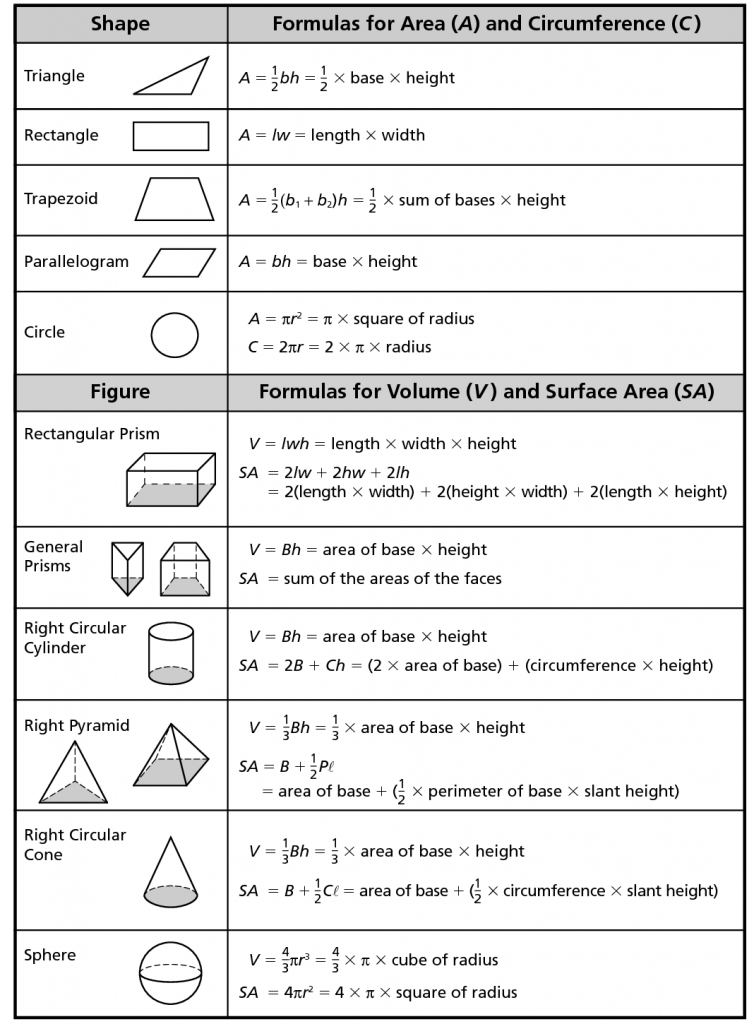
| Sl.No | Figure | Formula for surface area | Formula for volume |
| 1 | Rectangular Prism |
SA = 2ab+2bc+2ca sq. units
where a, b,c are the sides of the cube.
|
V = abc cubic units |
| 2 | Cylinder |
SA = 2πrh sq. units
TSA = 2πr(h+r) sq. units
r =radius of the cylinder
h – height of the cylinder
|
V = πr2h cubic units |
| 3 | Cube |
SA = 6a2 sq. units
a = sides of the cube
|
V = a3 cubic units |
| 4 | Sphere |
SA = 4πr2 sq. units
r = radius of the sphere
|
V = 4343πr3 cubic units |
| 5 | Ellipsoid |
SA = 4π[(apbp+apcp+bpcp)3]1p4π[(apbp+apcp+bpcp)3]1p
p = 1.6075
a, b, c are semi axis of ellipsoid
|
V = 4343 π r1,r2,r3 cubic units |
| 6 | Cone | CSA = πr1 sq.units | V = 1313πr2h cubic units |
| 7 | Pyramid |
SA = a+1212*p*l
p = perimeter of pyramid
l = slant height
a = area of the base of the pyramid
|
V = 1313*a*h cubic units |
| 8 | Torus |
SA = π2 * (R2 – r2)
R:Outer Radius
r: Inner Radius
|
V = 1414π3 (r1+r2) (r1-r2)2 cubic units |
| 9 | Hemisphere |
CSA = 2πr2
TSA = 3πr2
r = radius
|
V = 2323 πr3 cubic units |
| 10 | Triangle |
SA = s(s−a)(s−b)(s−c)‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√s(s−a)(s−b)(s−c)
where s is the perimeter of the triangle
a, b, c are the sides of the triangle
|
|
| 11 | Rectangle |
A = l*w
L = length
w = width
|
|
| 12 | Triangle |
A = 1212bh
b = base h = height
|
|
| 13 | Trapezoid | A = 1212 h (b1+b2) | |
| 14 | Parallelogram | A = bh | |
| 15 | Circle | A = πr2 r = radius |